The principal task of machine learning is to fit a model to some data. In programming terms, this model is an object with two methods:

class Model:

    def likelihood(self, x):
        pass

    def sample(self, n_samples):
        pass

Likelihood

How likely is the query point \(x\) under our model? In other words, how likely was it that our model produced \(x\)?

Note: The likelihood gives a value proportional to a valid probability, but is not necessarily a valid probability itself.

Sample

Draw a sample datum \(x\) from the model.

Notation

Canonically, we denote an instance of our Model in mathematical syntax as follows:

$$ x \sim p(x) $$

Again, this simple notation implies two powerful methods: that we can evaluate the likelihood of having observed \(x\) under our model \(p\), and that we can sample a new value \(x\) from our model \(p\).

Often, we work instead with conditional models, e.g. \(y \sim p(y\vert x)\), in classification and regression tasks. The likelihood and sample methods apply all the same.

Boltzmann machines

A Boltzmann machine is one of the simplest mechanisms for modeling \(p(x)\). It is an undirected graphical model where every dimension \(x_i\) of a given observation \(x\) influences every other dimension. As such, we might use it to model data which we believe to exhibit this property, e.g. an image (where intuitively, pixel values influence neighboring pixel values). For \(x \in R^3\), our model would look as follows:

png

For \(x \in R^n\), a given node \(x_i\) would have \(n - 1\) outgoing connections in total—one to every other node \(x_j\ \forall\ j \neq i\).

Finally, a Boltzmann machine strictly operates on binary data. This keeps things simple.

Computing the likelihood

A Boltzmann machines admits the following formula for computing the likelihood of data points \(x^{(1)}, ..., x^{(n)}\):

$$ H(x) = \sum\limits_{i \neq j} w_{i, j} x_i x_j + \sum\limits_i b_i x_i $$
$$ p(x) = \frac{\exp{(H(x))}}{Z} $$
$$ \mathcal{L}(x^{(1)}, ..., x^{(n)}) = \prod\limits_{i=1}^n p(x^{(i)}) $$

Note:

  • Since our weights can be negative, \(H(x)\) can be negative. Since our likelihood is proportional to a valid probability, we'd prefer it to be non-negative.
  • To enforce this constraint, we exponentiate \(H(x)\) in the second equation.
  • To normalize, we divide by the normalization constant \(Z\), i.e. the sum of the likelihoods of all possible values of \(x\).

Computing the partition function by hand

In the case of 2-dimensional binary datum \(x\), there are 4 possible "configurations": \([0, 0], [0, 1], [1, 0], [1, 1]\). As such, to compute the likelihood of one of these configurations, e.g.

$$ p([1, 0]) = \frac{\exp{(H([1, 0]))}}{\exp{(H([0, 0]))} + \exp{(H([0, 1]))} + \exp{(H([1, 0]))} + \exp{(H([1, 1]))}} $$

we see that the normalization constant \(Z\) is a sum of 4 terms.

More generally, given \(d\)-dimensional \(x\), where each \(x_i\) can assume one of \(v\) distinct values, computing \(p(x)\) implies a summation over \(v^d\) terms. With a non-trivially large \(v\) or \(d\) this becomes intractable to compute.

Below, we'll demonstrate how "tractability," i.e. "can we actually compute \(Z\) before the end of the universe?" changes with varying \(d\) for our Boltzmann machine (of \(v = 2\)).

The likelihood function in code

def _unnormalized_likelihood(self, x):
    return np.exp(self._H(x))

def _H(self, x):
    h = 0
    for i, j in self.var_combinations:
        h += self.weights[i, j] * x[i] * x[j]
    h += self.biases @ x
    return h

def likelihood(self, x, log=False):
    """
    :param x: a vector of shape (n_units,) or (n, n_units),
        where the latter is a matrix of multiple data points
        for which to compute the joint likelihood.
    """
    x = np.array(x)
    if x.shape[-1] != self.n_units:
        raise('Please pass 1 or more points of `n_units` dimensions')

    # compute unnormalized likelihoods
    multiple_samples = len(x.shape) == 2
    if multiple_samples:
        likelihood = [self._unnormalized_likelihood(point) for point in x]
    else:
        likelihood = [self._unnormalized_likelihood(x)]

    # compute partition function
    Z = sum([self._unnormalized_likelihood(config) for config in self.all_configs])

    if log:
        return sum([np.log(lik) - np.log(Z) for lik in likelihood])
    else:
        return reduce(np.multiply, [lik / Z for lik in likelihood])

NB: In mathematical Python code, for-loops are bad; we should prefer numpy instead. Nevertheless, I've used for-loops here because they are easier to read.

This code block is longer than you might expect because it includes a few supplementary behaviors, namely:

  • Computing the likelihood of one or more points
  • Avoiding redundant computation of Z
  • Optionally computing the log-likelihood

Training the model

At the outset, the parameters self.weights and self.biases of our model are initialized at random. Trivially, such that the values returned by likelihood and sample are useful, we must first update these parameters by fitting this model to observed data.

To do so, we will employ the principal of maximum likelihood: compute the parameters that make the observed data maximally likely under the model, via gradient ascent.

Gradients

Since our model is simple, we can derive exact gradients by hand. We will work with the log-likelihood instead of the true likelihood to avoid issues of computational underflow. Below, we simplify this expression, then compute its various gradients.

\(\log{\mathcal{L}}\)

$$ \mathcal{L}(x^{(1)}, ..., x^{(n)}) = \prod\limits_{k=1}^n \frac{\exp{(H(x^{(k)})}}{Z} $$
$$ \begin{align*} \log{\mathcal{L}(x^{(1)}, ..., x^{(n)})} &= \sum\limits_{k=1}^n \log{\frac{\exp{(H(x^{(k)})}}{Z}}\\ &= \sum\limits_{k=1}^n \log{\big(\exp{(H(x^{(k)})}\big)} - \log{Z}\\ &= \sum\limits_{k=1}^n H(x^{(k)}) - \log{Z} \end{align*} $$

This gives the total likelihood. Our aim is to maximize the expected likelihood with respect to the data generating distribution.

Expected likelihood

$$ \begin{align*} \mathop{\mathbb{E}}_{x \sim p_{\text{data}}}\big[ \mathcal{L}(x) \big] &= \sum\limits_{k=1}^N p_{\text{data}}(x = x^{(k)}) \mathcal{L(x^{(k)})}\\ &\approx \sum\limits_{k=1}^N \frac{1}{N} \mathcal{L(x^{(k)})}\\ &= \frac{1}{N} \sum\limits_{k=1}^N \mathcal{L(x^{(k)})}\\ \end{align*} $$

In other words, we wish to maximize the average likelihood of our data under the model. Henceforth, we will refer to this quantity as \(\mathcal{L}\), i.e. \(\mathcal{L} = \frac{1}{N} \sum\limits_{k=1}^n H(x^{(k)}) - \log{Z}\).

Now, deriving the gradient with respect to our weights:

\(\nabla_{w_{i, j}}\log{\mathcal{L}}\):

$$ \begin{align*} \nabla_{w_{i, j}} \frac{1}{N} \sum\limits_{k=1}^n H(x^{(k)}) - \log{Z} &= \frac{1}{N} \sum\limits_{k=1}^n \nabla_{w_{i, j}} H(x^{(k)}) - \frac{1}{N} \sum\limits_{k=1}^n \nabla_{w_{i, j}} \log{Z} \end{align*} $$

First term:

$$ \begin{align*} \frac{1}{N} \sum\limits_{k=1}^n \nabla_{w_{i, j}} H(x^{(k)}) &= \frac{1}{N} \sum\limits_{k=1}^n \nabla_{w_{i, j}} \bigg[ \sum\limits_{i \neq j} w_{i, j} x_i^{(k)} x_j^{(k)} + \sum\limits_i b_i x_i^{(k)} \bigg]\\ &= \frac{1}{N} \sum\limits_{k=1}^n x_i^{(k)} x_j^{(k)}\\ &\approx \mathop{\mathbb{E}}_{x \sim p_{\text{data}}} [x_i x_j] \end{align*} $$

Second term:

NB: \(\sum\limits_{\mathcal{x}}\) implies a summation over all \(v^d\) possible configurations of \(x\).

$$ \begin{align*} \nabla_{w_{i, j}} \log{Z} &= \nabla_{w_{i, j}} \log{\sum\limits_{\mathcal{x}}} \exp{(H(x))}\\ &= \frac{1}{\sum\limits_{\mathcal{x}} \exp{(H(x))}} \nabla_{w_{i, j}} \sum\limits_{\mathcal{x}} \exp{(H(x))}\\ &= \frac{1}{Z} \sum\limits_{\mathcal{x}} \nabla_{w_{i, j}} \exp{(H(x))}\\ &= \frac{1}{Z} \sum\limits_{\mathcal{x}} \exp{(H(x))} \nabla_{w_{i, j}} H(x)\\ &= \sum\limits_{\mathcal{x}} \frac{\exp{(H(x))}}{Z} \nabla_{w_{i, j}} H(x)\\ &= \sum\limits_{\mathcal{x}} p(x) \nabla_{w_{i, j}} H(x)\\ &= \sum\limits_{\mathcal{x}} p(x) [x_i x_j]\\ &= \mathop{\mathbb{E}}_{x \sim p_{\text{model}}} [x_i x_j] \end{align*} $$

Putting it back together

Combining these constituent parts, we arrive at the following formula:

$$ \nabla_{w_{i, j}}\log{\mathcal{L}} = \mathop{\mathbb{E}}_{x \sim p_{\text{data}}} [x_i x_j] - \mathop{\mathbb{E}}_{x \sim p_{\text{model}}} [x_i x_j] $$

Finally, following the same logic, we derive the exact gradient with respect to our biases:

$$ \nabla_{b_i}\log{\mathcal{L}} = \mathop{\mathbb{E}}_{x \sim p_{\text{data}}} [x_i] - \mathop{\mathbb{E}}_{x \sim p_{\text{model}}} [x_i] $$

The first and second terms of each gradient are called, respectively, the positive and negative phases.

Computing the positive phase

In the following toy example, our data are small: we can compute the positive phase using all of the training data, i.e. \(\frac{1}{N} \sum\limits_{k=1}^n x_i^{(k)} x_j^{(k)}\). Were our data bigger, we could approximate this expectation with a mini-batch of training data (much like SGD).

Computing the negative phase

Again, this term asks us to compute then sum the log-likelihood over every possible data configuration in the support of our model, which is \(O(v^d)\). With non-trivially large \(v\) or \(d\), this becomes intractable to compute.

Below, we'll begin our toy example by computing the true negative-phase, \(\mathop{\mathbb{E}}_{x \sim p_{\text{model}}} [x_i x_j]\), with varying data dimensionalities \(d\). Then, once this computation becomes slow, we'll look to approximate this expectation later on.

Parameter updates in code

def update_parameters_with_true_negative_phase(weights, biases, var_combinations, all_configs, data, alpha=alpha):
    model = Model(weights, biases, var_combinations, all_configs)
    model_distribution = [(np.array(config), model.likelihood(config)) for config in all_configs]

    for i, j in var_combinations:
        # positive phase
        positive_phase = (data[:, i] * data[:, j]).mean()

        # negative phase
        negative_phase = sum([config[i] * config[j] * likelihood for config, likelihood in model_distribution])

        # update weights
        weights[i, j] += alpha * (positive_phase - negative_phase)

    for i, _ in enumerate(biases):
        # positive phase
        positive_phase = data[:, i].mean()

        # negative phase
        negative_phase = sum([config[i] * likelihood for config, likelihood in model_distribution])

        # update biases
        biases[i] += alpha * (positive_phase - negative_phase)

    return np.array(weights), np.array(biases)

Train model, visualize model distribution

Finally, we're ready to train. Using the true negative phase, let's train our model for 100 epochs with \(d=3\) then visualize results.

seed = 42
alpha = .01


def reset_data_and_parameters(n_units=3, n_obs=100, p=[.8, .1, .5]):
    """
    Generate training data, weights, biases, and a list of all data configurations
    in our model's support.

    In addition, generate a list of tuples of the indices of adjacent nodes, which
    we'll use to update parameters without duplication.

    For example, with `n_units=3`, we generate a matrix of weights with shape (3, 3);
    however, there are only 3 distinct weights in this matrix that we'll actually
    want to update: those connecting Node 0 --> Node 1, Node 1 --> Node 2, and
    Node 0 --> Node 2. This function returns a list containing these tuples
    named `var_combinations`.

    :param n_units: the dimensionality of our data `d`
    :param n_obs: the number of observations in our training set
    :param p: a vector of the probabilities of observing a 1 in each index
        of the training data. The length of this vector must equal `n_units`

    :return: weights, biases, var_combinations, all_configs, data
    """
    np.random.seed(seed)

    # initialize data
    data = np.random.binomial(n=1, p=p, size=(100, n_units))

    # initialize parameters
    biases = np.random.randn(n_units)
    weights = np.random.randn(n_units, n_units)

    # a few other pieces we'll need
    var_combinations = list(combinations(range(n_units), 2))
    all_configs = list(product([0, 1], repeat=n_units))

    return weights, biases, var_combinations, all_configs, data


class Model:

    def __init__(self, weights, biases, var_combinations, all_configs):
        self.weights = weights
        self.biases = biases
        self.var_combinations = var_combinations
        self.all_configs = all_configs
        self.n_units = len(self.biases)

    @staticmethod
    def _inv_logit(z):
        return 1 / (1 + np.exp(-z))

    def _unnormalized_likelihood(self, x):
        return np.exp(self._H(x))

    def _H(self, x):
        h = 0
        for i, j in self.var_combinations:
            h += self.weights[i, j] * x[i] * x[j]
        h += self.biases @ x
        return h

    def likelihood(self, x, log=False):
        """
        :param x: a vector of shape (n_units,) or (n, n_units),
            where the latter is a matrix of multiple data points
            for which to compute the joint likelihood.
        """
        x = np.array(x)
        if x.shape[-1] != self.n_units:
            raise('Please pass 1 or more points of `n_units` dimensions')

        # compute unnormalized likelihoods
        multiple_samples = len(x.shape) == 2
        if multiple_samples:
            likelihood = [self._unnormalized_likelihood(point) for point in x]
        else:
            likelihood = [self._unnormalized_likelihood(x)]

        # compute partition function
        Z = sum([self._unnormalized_likelihood(config) for config in self.all_configs])

        if log:
            return sum([np.log(lik) - np.log(Z) for lik in likelihood])
        else:
            return reduce(np.multiply, [lik / Z for lik in likelihood])

    def sample(self, n_samples=100, init_sample=None, burn_in=25, every_n=10, seed=seed) -> np.array:

        np.random.seed(seed)

        if burn_in > n_samples:
            raise("Can't burn in for more samples than there are in the chain")

        init_sample = init_sample or [0 for _ in self.biases]
        samples = [init_sample]

        def _gibbs_step(sample, i):
            z = sum([self.weights[i, j] * sample[j] for j in range(len(sample)) if j != i]) + self.biases[i]
            p = self._inv_logit(z)
            return np.random.binomial(n=1, p=p)

        for _ in range(n_samples):
            sample = list(samples[-1])  # make copy
            for i, _ in enumerate(sample):
                sample[i] = _gibbs_step(sample=sample, i=i)
            samples.append( sample )

        return np.array([sample for i, sample in enumerate(samples[burn_in:]) if i % every_n == 0])


def update_parameters_with_true_negative_phase(weights, biases, var_combinations, all_configs, data, alpha=alpha, **kwargs):
    model = Model(weights, biases, var_combinations, all_configs)
    model_distribution = [(np.array(config), model.likelihood(config)) for config in all_configs]

    for i, j in var_combinations:
        # positive phase
        positive_phase = (data[:, i] * data[:, j]).mean()

        # negative phase
        negative_phase = sum([config[i] * config[j] * likelihood for config, likelihood in model_distribution])

        # update weights
        weights[i, j] += alpha * (positive_phase - negative_phase)

    for i, _ in enumerate(biases):
        # positive phase
        positive_phase = data[:, i].mean()

        # negative phase
        negative_phase = sum([config[i] * likelihood for config, likelihood in model_distribution])

        # update biases
        biases[i] += alpha * (positive_phase - negative_phase)

    return np.array(weights), np.array(biases)

Train

weights, biases, var_combinations, all_configs, data = reset_data_and_parameters(n_units=3, p=[.8, .1, .5])


for i in range(100):
    weights, biases = update_parameters_with_true_negative_phase(weights, biases, var_combinations, all_configs, data, alpha=1)

    lik = Model(weights, biases, var_combinations, all_configs).likelihood(data, log=True)
    if i % 10 == 0:
        print(f'Epoch: {i:2} | Likelihood: {lik}')

Epoch:  0 | Likelihood: -209.63758306786653
Epoch: 10 | Likelihood: -162.04280784271083
Epoch: 20 | Likelihood: -160.49961381649555
Epoch: 30 | Likelihood: -159.79539070373576
Epoch: 40 | Likelihood: -159.2853717231018
Epoch: 50 | Likelihood: -158.90186293631422
Epoch: 60 | Likelihood: -158.6084020645482
Epoch: 70 | Likelihood: -158.38094343579155
Epoch: 80 | Likelihood: -158.20287017780586
Epoch: 90 | Likelihood: -158.06232196551673

Visualize samples

def plot_n_samples(n_samples, weights, biases):
    """
    NB: We add some jitter to the points so as to better visualize density in a given corner of the model.
    """
    fig = plt.figure(figsize=(12, 9))
    ax = fig.add_subplot(111, projection='3d')

    samples = Model(weights, biases, var_combinations, all_configs).sample(n_samples)
    x, y, z = zip(*np.array(samples))

    x += np.random.randn(len(x)) * .05
    y += np.random.randn(len(y)) * .05
    z += np.random.randn(len(z)) * .05

    ax.scatter(x, y, z)
    ax.set_xlabel('Node 0')
    ax.set_ylabel('Node 1')
    ax.set_zlabel('Node 2')

n_samples = 1000

plot_n_samples(n_samples, weights, biases)
_ = plt.title(f'{n_samples} Samples from Model')

png

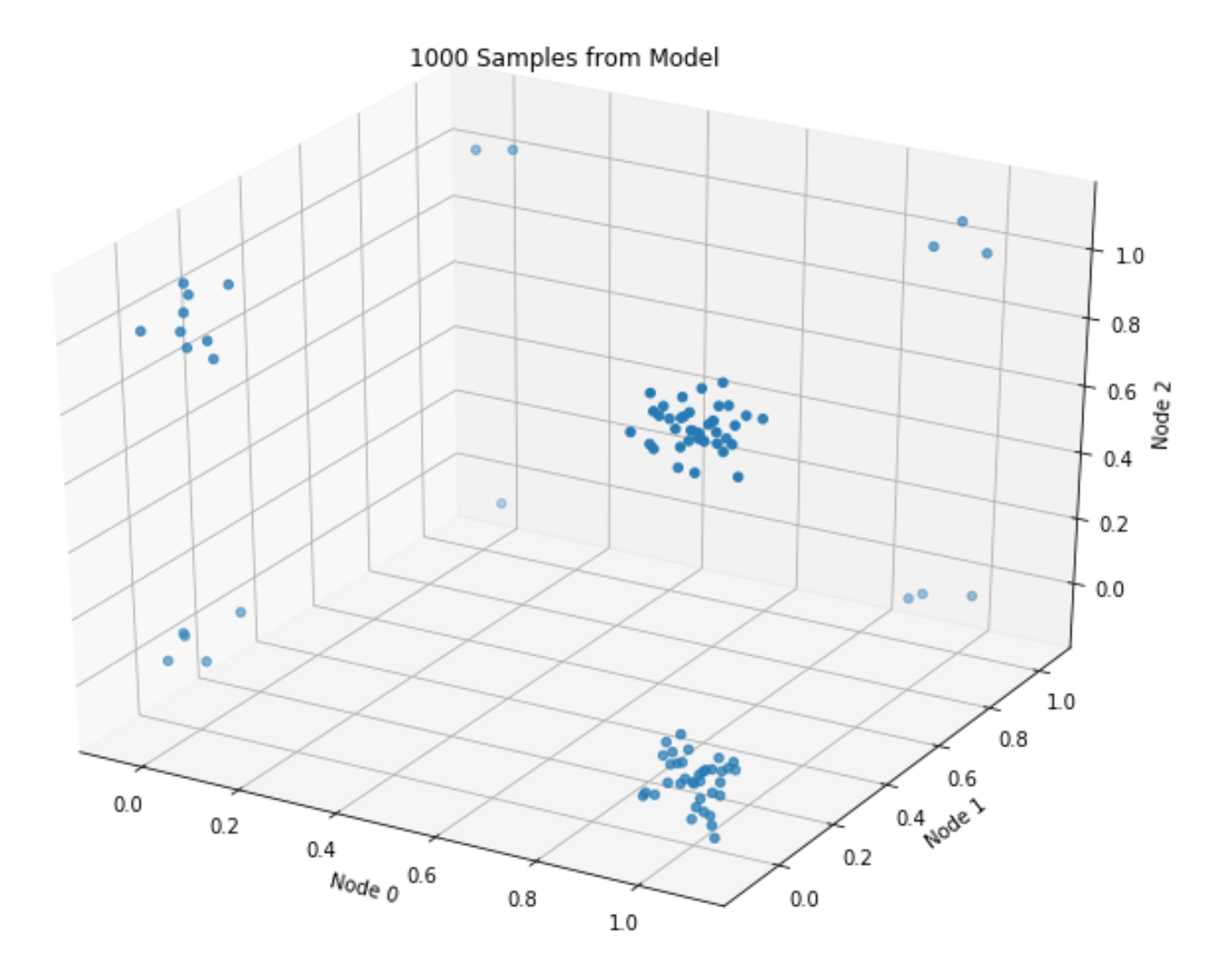
The plot roughly matches the data-generating distribution: most points assume values of either \([1, 0, 1]\), or \([1, 0, 0]\) (given \(p=[.8, .1, .5]\)).

Sampling, via Gibbs

The second, final method we need to implement is sample. In a Boltzmann machine, we typically do this via Gibbs sampling.

To effectuate this sampling scheme, we'll need a model of each data dimension conditional on the other data dimensions. For example, for \(d=3\), we'll need to define:

  • \(p(x_0\vert x_1, x_2)\)
  • \(p(x_1\vert x_0, x_2)\)
  • \(p(x_2\vert x_0, x_1)\)

Given that each dimension must assume a 0 or a 1, the above 3 models must necessarily return the probability of observing a 1 (where 1 minus this value gives the probability of observing a 0).

Let's derive these models using the workhorse axiom of conditional probability, starting with the first:

$$ \begin{align*} p(x_0 = 1\vert x_1, x_2) &= \frac{p(x_0 = 1, x_1, x_2)}{p(x_1, x_2)}\\ &= \frac{p(x_0 = 1, x_1, x_2)}{\sum\limits_{x_0 \in [0, 1]} p(x_0, x_1, x_2)}\\ &= \frac{p(x_0 = 1, x_1, x_2)}{p(x_0 = 0, x_1, x_2) + p(x_0 = 1, x_1, x_2)}\\ &= \frac{1}{1 + \frac{p(x_0 = 0, x_1, x_2)}{p(x_0 = 1, x_1, x_2)}}\\ &= \frac{1}{1 + \frac{\exp{(H(x_0 = 0, x_1, x_2)))}}{\exp{(H(x_0 = 1, x_1, x_2)))}}}\\ &= \frac{1}{1 + \exp{(H(x_0 = 0, x_1, x_2) - H(x_0 = 1, x_1, x_2))}}\\ &= \frac{1}{1 + \exp{(\sum\limits_{i \neq j} w_{i, j} x_i x_j + \sum\limits_i b_i x_i - (\sum\limits_{i \neq j} w_{i, j} x_i x_j + \sum\limits_i b_i x_i))}}\\ &= \frac{1}{1 + \exp{(-\sum\limits_{j \neq i = 0} w_{i, j} x_j - b_i)}}\\ &= \sigma\bigg(\sum\limits_{j \neq i = 0} w_{i, j} x_j + b_i\bigg)\\ \end{align*} $$

Pleasantly enough, this model resolves to a simple Binomial GLM, i.e. logistic regression, involving only its neighboring units and the weights that connect them.

With the requisite conditionals in hand, let's run this chain and compare it with our (trained) model's true probability distribution.

True probability distribution

model = Model(weights, biases, var_combinations, all_configs)

distribution = [(np.array(config), model.likelihood(config)) for config in all_configs]
assert sum([likelihood for config, likelihood in distribution]) == 1

for config, likelihood in distribution:
    print(f'{list(config)}: {likelihood:.4}')

[0, 0, 0]: 0.07327
[0, 0, 1]: 0.09227
[0, 1, 0]: 0.01366
[0, 1, 1]: 0.01938
[1, 0, 0]: 0.3351
[1, 0, 1]: 0.3622
[1, 1, 0]: 0.04693
[1, 1, 1]: 0.05715

Empirical probability distribution, via Gibbs

empirical_dist = defaultdict(int)
samples = model.sample(n_samples=1000)
n_samples = len(samples)

for sample in samples:
    empirical_dist[tuple(sample)] += 1 / n_samples
assert np.round(sum(empirical_dist.values()), 8) == 1

for config, likelihood in distribution:
    empirical_probability = empirical_dist[tuple(config)]
    print(f'{list(config)}: {likelihood:.4} (true), {empirical_probability:.4} (empirical)')

[0, 0, 0]: 0.07327 (true), 0.05102 (empirical)
[0, 0, 1]: 0.09227 (true), 0.09184 (empirical)
[0, 1, 0]: 0.01366 (true), 0.0102 (empirical)
[0, 1, 1]: 0.01938 (true), 0.02041 (empirical)
[1, 0, 0]: 0.3351 (true), 0.3673 (empirical)
[1, 0, 1]: 0.3622 (true), 0.398 (empirical)
[1, 1, 0]: 0.04693 (true), 0.03061 (empirical)
[1, 1, 1]: 0.05715 (true), 0.03061 (empirical)

Close, ish enough.

Scaling up, and hitting the bottleneck

With data of vary dimensionality n_units, the following plot gives the time in seconds that it takes to train this model for 10 epochs.

png

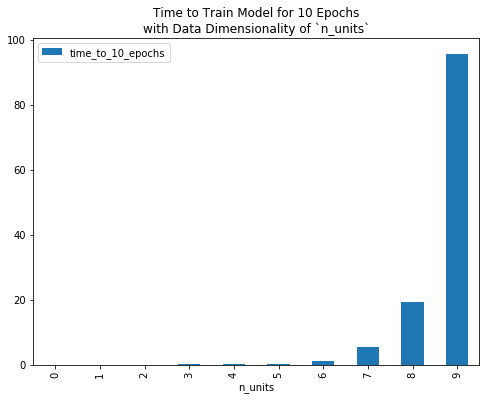
To reduce computational burden, and/or to fit a Boltzmann machine to data of non-trivial dimensionality (e.g. a 28x28 grey-scale image, which implies a random variable with 28x28=784 dimensions), we need to compute the positive and/or negative phase of our gradient faster than we currently are.

To compute the former more quickly, we could employ mini-batches as in canonical stochastic gradient descent.

In this post, we'll instead focus on ways to speed up the latter. Revisiting its expression, \(\mathop{\mathbb{E}}_{x \sim p_{\text{model}}} [x_i x_j]\), we readily see that we can create an unbiased estimator for this value by drawing Monte Carlo samples from our model, i.e.

$$ \mathop{\mathbb{E}}_{x \sim p_{\text{model}}} [x_i x_j] \approx \frac{1}{N}\sum\limits_{k=1}^N x^{(k)}_i x^{(k)}_j\quad\text{where}\quad x^{(k)} \sim p_{\text{model}} $$

So, now we just need a way to draw these samples. Luckily, we have a Gibbs sampler to tap!

Instead of computing the true negative phase, i.e. summing \(x_i x_j\) over all permissible configurations \(X\) under our model, we can approximate it by evaluating this expression for a few model samples, then taking the mean.

We define this update mechanism here:

def update_parameters_with_gibbs_sampling(weights, biases, var_combinations, all_configs, data,
                                          seed=42, n_samples=1000, alpha=alpha, **kwargs):
    model_samples = Model(weights, biases, var_combinations, all_configs).sample(n_samples=n_samples, seed=seed)

    for i, j in var_combinations:
        # positive phase
        positive_phase = (data[:, i] * data[:, j]).mean()

        # negative phase
        negative_phase = (model_samples[:, i] * model_samples[:, j]).mean()

        # update weights
        weights[i, j] += alpha * (positive_phase - negative_phase)

    for i, _ in enumerate(biases):
        # positive phase
        positive_phase = data[:, i].mean()

        # negative phase
        negative_phase = model_samples[:, i].mean()

        # update biases
        biases[i] += alpha * (positive_phase - negative_phase)

    return np.array(weights), np.array(biases)

Next, we'll define a function that we can parameterize by an optimization algorithm (computing the true negative phase, or approximating it via Gibbs sampling, in the above case) which will train a model for \(n\) epochs and return data requisite for plotting.

How does training progress for varying data dimensionalities?

Finally, for data of n_units 3, 4, 5, etc., let’s train models for 100 epochs and plot likelihood curves.

When training with the approximate negative phase, we’ll:

  • Derive model samples from a 1000-sample Gibbs chain. Of course, this is a parameter we can tune, which will affect both model accuracy and training runtime. However, we don’t explore that in this post; instead, we just pick something reasonable and hold this value constant throughout our experiments.
  • Train several models for a given n_units; Seaborn will average results for us then plot a single line.
all_updates = []
alpha = .1
min_units, max_units = 3, 7

for n_units in range(min_units, max_units):

    np.random.seed(n_units)
    p = np.random.uniform(size=n_units)
    n_epochs = 100

    if n_units % 5 == 0:
        alpha /= 10

    for run in range(5):
        updates = train_model_for_n_epochs(
            update_parameters_with_gibbs_sampling,
            n_units=n_units,
            epochs=100,
            verbose=False,
            alpha=alpha,
            run_num=run+1,
            p=p
        )
        all_updates.append(updates.assign(n_units=n_units))


    for run in range(1):
        updates = train_model_for_n_epochs(
            update_parameters_with_true_negative_phase,
            n_units=n_units,
            epochs=100,
            verbose=False,
            alpha=alpha,
            run_num=run+1,
            p=p
        )
        all_updates.append(updates.assign(n_units=n_units))

Plot

png

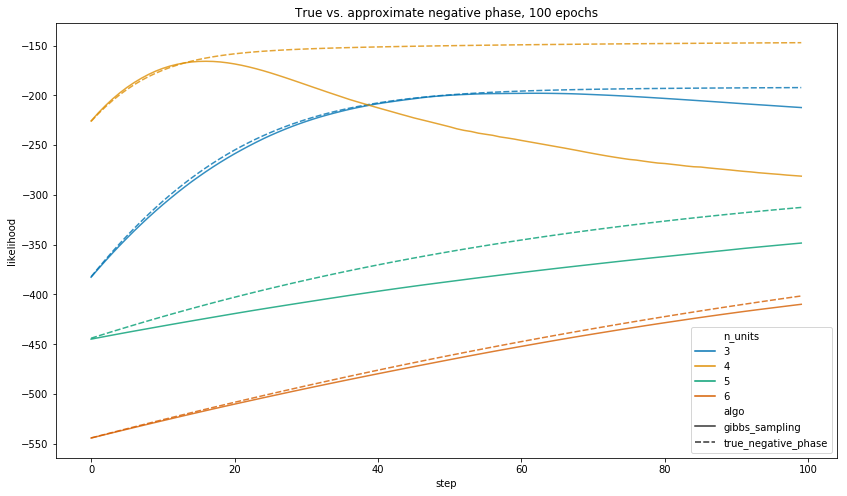
When we let each algorithm run for 100 epochs, the true negative phase gives a model which assigns higher likelihood to the observed data in all of the above training runs.

Notwithstanding, the central point is that 100 epochs of the true negative phase takes a long time to run.

As such, let’s run each for an equal amount of time, and plot results. Below, we define a function to train models for \(n\) seconds (or 1 epoch—whichever comes first).

all_updates = []
n_seconds = 1
alpha = .1
min_units, max_units = 3, 10

for n_units in range(min_units, max_units):

    np.random.seed(n_units)
    p = np.random.uniform(size=n_units)
    n_epochs = 100

    if n_units % 5 == 0:
        alpha /= 10

    for run in range(5):
        updates = train_model_for_n_seconds(
            update_parameters_with_gibbs_sampling,
            n_units=n_units,
            n_seconds=n_seconds,
            verbose=False,
            alpha=alpha,
            run_num=run+1,
            p=p
        )
        all_updates.append(updates.assign(n_units=n_units))


    for run in range(1):
        updates = train_model_for_n_seconds(
            update_parameters_with_true_negative_phase,
            n_units=n_units,
            n_seconds=n_seconds,
            verbose=False,
            alpha=alpha,
            run_num=run+1,
            p=p
        )
        all_updates.append(updates.assign(n_units=n_units))

How many epochs do we actually get through?

Before plotting results, let’s examine how many epochs each algorithm completes in its allotted time. In fact, for some values of n_units, we couldn’t even complete a single epoch (when computing the true negative phase) in \(\leq 1\) second.

png

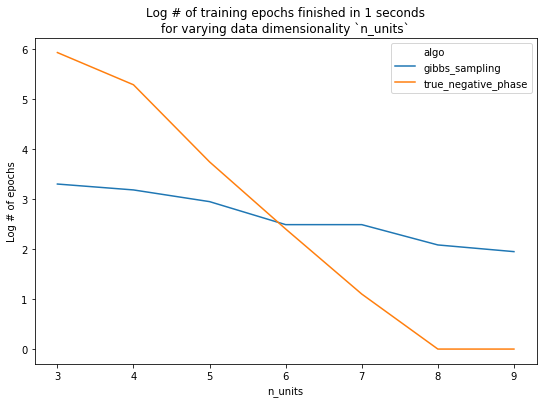
Finally, we look at performance. With n_units <= 7, we see that 1 second of training with the true negative phase yields a better model. Conversely, using 7 or more units, the added performance given by using the true negative phase is overshadowed by the amount of time it takes the model to train.

Plot

png

Of course, we re-stress that the exact ablation results are conditional (amongst other things) on the number of Gibbs samples we chose to draw. Changing this will change the results, but not that about which we care the most: the overall trend.

Summary

Throughout this post, we've given a thorough introduction to a Boltzmann machine: what it does, how it trains, and some of the computational burdens and considerations inherent.

In the next post, we'll look at cheaper, more inventive algorithms for avoiding the computation of the negative phase, and describe how they're used in common machine learning models and training routines.

Code

The repository and rendered notebook for this project can be found at their respective links.

References

  1. CSC321 Lecture 19: Boltzmann Machines ↩

  2. Derivation: Maximum Likelihood for Boltzmann Machines ↩

  3. Boltzmann Machines ↩